LES MULTIPLICATIONS ET LES DIVISIONS PAR L’IMPRESSION
PROJET
Créer un outil d’impression inspiré des motifs utilisés par les artistes des Premières Nations et imprimer les tables de multiplication.
LE CHIFFRE 8 — Argile, 4 x 3 x 3 pouces.
.
Adaptation scolaire, classe de Zéa Blackburn, école Jean-Du-Nord, Sept-Îles (Québec), 2018-2019
.
Bien que les cours s’étendent généralement sur trois sessions d’une heure chacune, ce cours créé pour des jeunes en adaptation scolaire, s’étend sur quatre heures à raison d’une heure vingt minutes chacune.
MATÉRIEL
LE MATÉRIEL D’ART EST FOURNI PAR ETAPMANITU
1. Papier régulier, 11 x 17 po (1 par élève)
2. Crayon à mine, gomme à effacer et crayon-feutre noir (1 par élève)
3. Cartons de couleurs variées, 11 x 17 po (1 par élève)
4. Papier à masquer (collant)
5. Encre de Chine et assiette (1 par élève)
6. Petits contenants d’eau (1 pour 2 élèves)
7. Argile 2 x 4 x 2 po (1 par élève)
8. Couteau de plastique (1 par élève)
9. Plastique (recouvrir les tables) et papier brun ou papier journal (essais)
10. Tablier (1 par élève)
.
LANGAGE PLASTIQUE
Geste : graver
Matériaux : argile, encre
Organisation de l’espace : symétrie, asymétrie
Techniques : sculpture, impression
Volume : forme tridimensionnelle
Vocabulaire : division, figure symétrique, multiplication, surface, volume
.
OUTILS PÉDAGOGIQUES
Vidéo sur le mode de vie innu – Enseignement traditionnel – Production Manitu inc.
Organisation partage – Durée : 4 min 32 s.
.
.
CHIFFRES ET SYMBOLES
.
Exercices de symétrie (à imprimer)
.
.
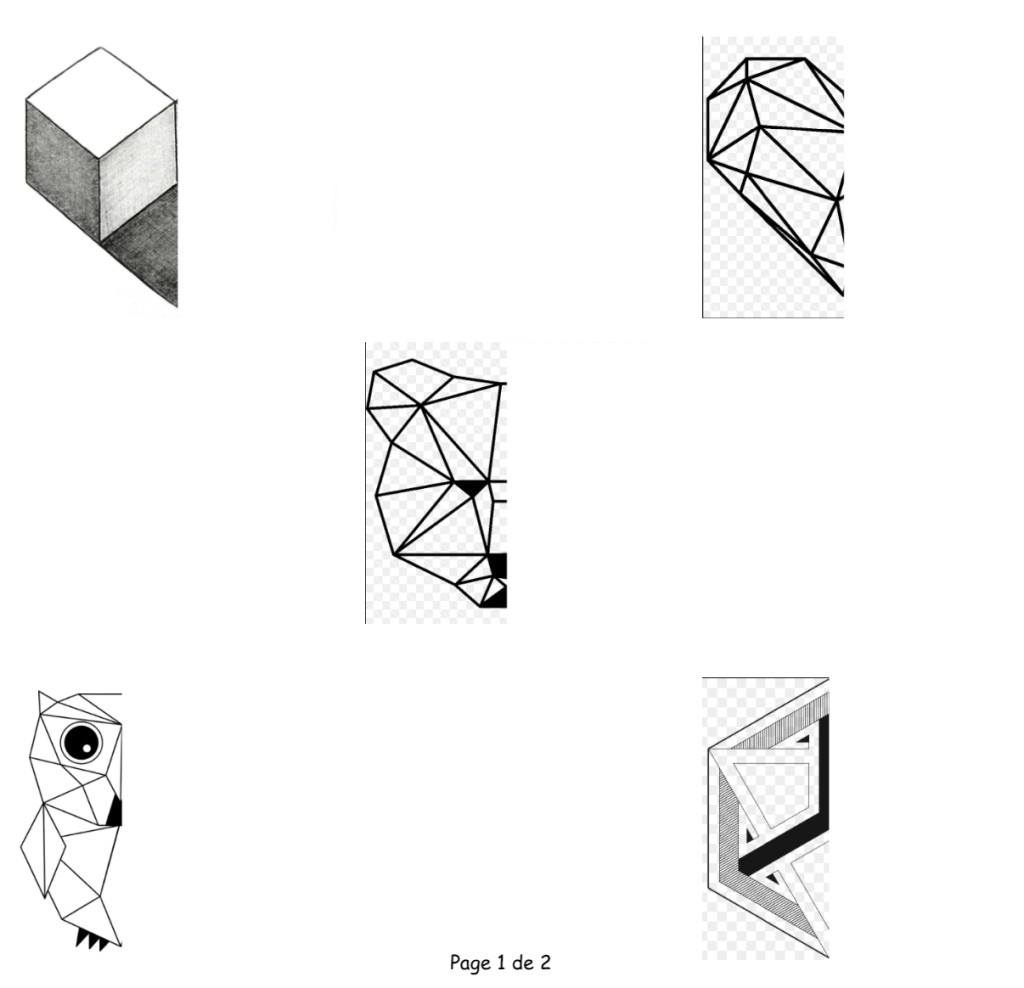
Carnet de traces
.
.
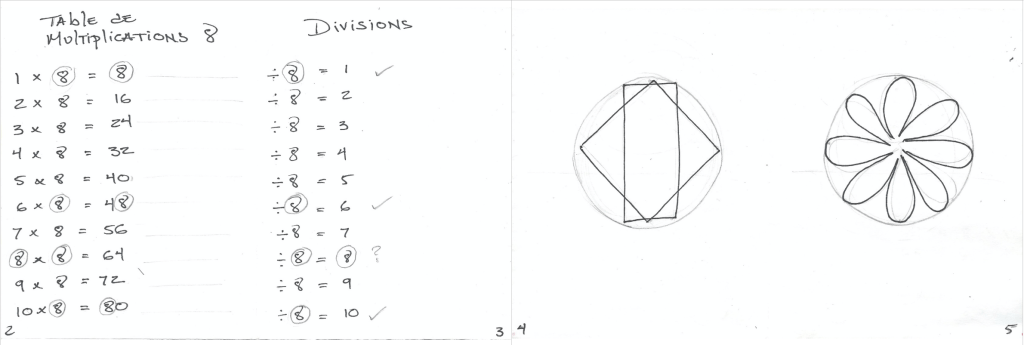
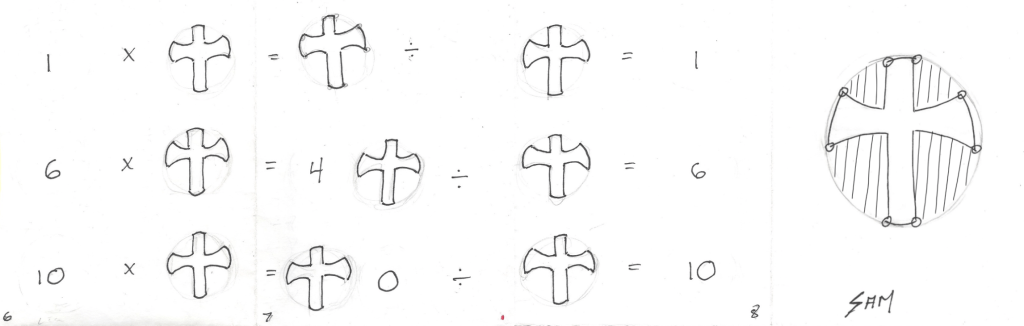
Ce projet est financé par le ministère de l’Éducation et de l’Enseignement supérieur du Québec.
.
.
CONTENU DU CARNET DE TRACES
Les élèves fabriquent un carnet de traces de 8 pages et compilent les informations suivantes :
PAGE COUVERTURE : écrire son nom en bas, au centre ; dessiner un symbole à l’intérieur d’un cercle ; hachurer les zones négatives.
Page 2 : écrire la table de multiplication qui se réfère à son nombre.
Page 3 : écrire les divisions qui se réfèrent à la table de multiplication.
Page 4 : dessiner un symbole à l’intérieur d’un cercle.
Page 5 : dessiner un deuxième symbole à l’intérieur d’un cercle.
Page 6 : tracer six cercles (deux en haut, deux au centre et deux en bas).
Page 7 : écrire des nombres à l’intérieur des cercles et ajouter les symboles (= et ÷).
Page 8 : écrire un nombre ; remplacer un nombre par un symbole.
Démonstration — Réalisation d’un carnet de traces – Durée : 48 s.
.
ÉTAPES DU COURS
Jour 1
PRÉPARATION
Préparer sur le TBI (tableau blanc interactif) :
– la vidéo sur le mode de vie innu pour le visionnement
– les symboles appartenant à différentes cultures.
.
.
Distribuer à chaque élève un papier régulier, 11 x 17 pouces.
.
1. Présenter l’artiste et le projet. Qu’est-ce que l’encre de Chine ? Réputée venir d’Orient, de Chine ou d’Inde, cette encre associe un pigment noir de carbone et un liant aqueux ; une encre noire utilisée pour l’écriture, le dessin et la peinture au lavis.
2. Visionner la vidéo sur le mode de vie innu — Organisation partage — Production Manitu inc. Durée : 4 min 32 s.
3. L’élève réalise un carnet de traces en manipulant et en pliant un papier de 11 x 17 pouces, en 8 carrés égaux. Il repère la page couverture et écrit son nom au bas de la page. Il numérote ensuite les pages de 2 à 8 dans les coins extérieurs au bas de chaque page.
4. Écrire les nombres de 2 à 12 sur des bouts de papier. À tour de rôle, piger un nombre et l’écrire en haut de la page 2. Le 0 et le 1 seront tracés à main levée. (Pour plus de onze élèves, diviser la classe en deux.)
5. Écrire la table de multiplication qui se réfère à son nombre (p. ex. : 1 x 8 = 8, etc.), page 2. Écrire les divisions qui se réfèrent aux réponses (p. ex. : 8 ÷ 8 = 1, etc.), page 3.
6. Qu’est-ce qu’un symbole ? C’est un concept, une représentation pensée chez un individu en particulier ou un groupe en général (ex. : le « M » de McDonald). Consulter les symboles appartenant à différentes cultures, à travers les époques (sur le TBI).
7. Qu’est-ce que l’asymétrie ? C’est l’absence de symétrie. Dessiner la moitié d’un symbole au tableau, puis inviter un élève à le finaliser en spécifiant que l’on veut compléter un symbole asymétrique ! Et qui peut dessiner le symbole arabe du 9 ?
Entre le jour 1 et le jour 2
– L’enseignant s’assure de la compréhension de l’élève et vérifie que la collecte de l’information est conforme aux attentes : table de multiplication (page 2), équations, divisions (page 3).
Jour 2
PRÉPARATION
Imprimer les exercices de symétrie, format env. 3 x 3 po (1 par élève).
.
Couper des morceaux d’argile, format env. 2 x 4 x 2 po (1 par élève).
Bien que l’argile se lave facilement à l’eau, il vaut mieux recouvrir les tables.
Redonner à chaque élève son carnet de traces.
Distribuer à chaque élève :
– une photocopie d’exercices de symétrie
– un morceau d’argile
– un couteau de plastique
– un tablier.
.
8. Dessiner la moitié d’un symbole au tableau, puis inviter un pair à le finaliser symétriquement. Ensuite, choisir et compléter un ou plusieurs exercices sur la symétrie.
.
9. Réaliser son symbole afin d’illustrer son nombre — Dessiner des symboles au tableau, à l’intérieur d’un cercle : le symbole doit avoir le même nombre de pointes que son nombre et DOIT ÊTRE SYMÉTRIQUE ou très près (p. ex. : le nombre 8, une fleur à huit pétales). Ce sont les pointes qui touchent au cercle qui déterminent le nombre. Tracer à main levée. Refaire le même exercice, pages 4 et 5, en utilisant d’autres idées graphiques.
.
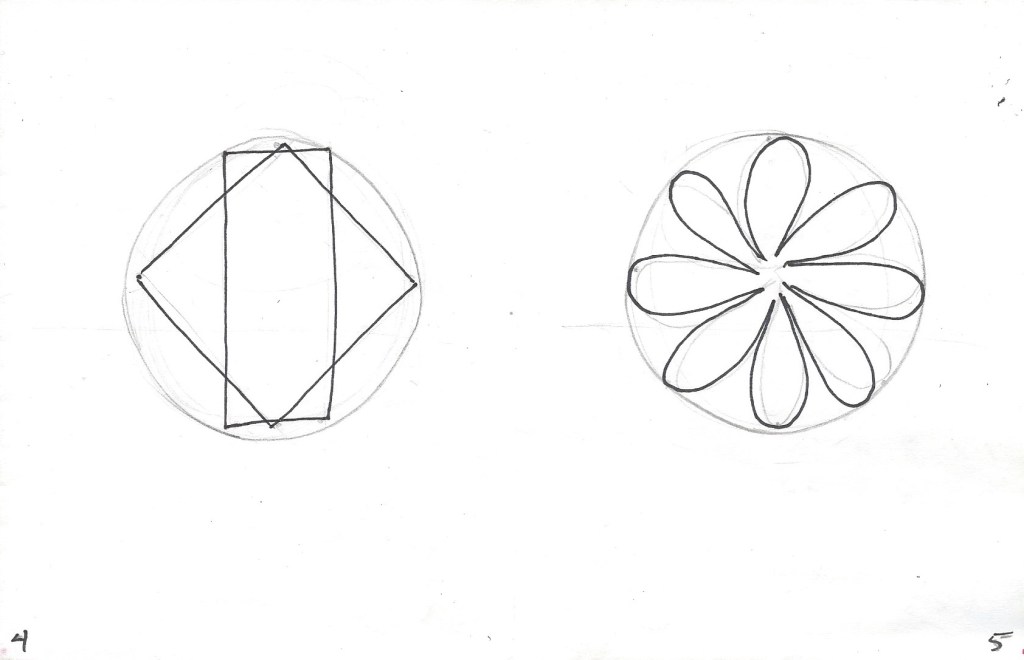
10. Choisir trois équations (voir pages 2 et 3) dans lesquelles se retrouve son nombre plus d’une fois (p. ex. : 1 x 8 = 8 ÷ 8 = 1 // 6 x 8 = 48 ÷ 8 = 6 // 10 x 8 = 80 ÷ 8 = 10). Tracer un petit crochet à la fin des trois équations choisies.
.
11. Tracer six cercles, deux en haut, deux au centre et deux en bas de la page (p. ex. : 1 x 8 ; écrire 1 dans le premier cercle et remplacer 8 par le symbole), page 6. Continuer l’équation, page 7 (p. ex. : = 8), écrire ensuite la fin de l’équation (p. ex. : 8 = 1), page 8.
.
12. Choisir un des deux symboles OU en réaliser un nouveau et le dessiner avec plus de précision sur la page couverture. Repérer les zones négatives et positives et hachurer les zones négatives.
.
13. Démonstration — Aplanir un morceau d’argile, tracer le symbole à l’aide d’un crayon à mine et enlever les zones négatives à l’aide d’un petit couteau de plastique.
Entre le jour 2 et le jour 3
– L’enseignant s’assure que les éléments suivants figurent dans les carnets de traces : deux symboles (pages 4 et 5 et page couverture), trois équations (pages 6, 7 et 8).
– L’élève retrace les lignes de contour de son symbole final au crayon-feutre noir. (Pour éviter les taches, placer un papier entre la page couverture et la page 2.)
Jour 3
PRÉPARATION
Placer les tables de façon à ce que les élèves soient côte à côte (en cercle ou face à face).
L’encre de Chine tache, il vaut mieux recouvrir les tables ; bien agiter le contenant avant d’ouvrir.
Verser une petite quantité d’encre de Chine dans des assiettes (1 par table). Redonner de l’encre pendant le cours, si nécessaire.
Redonner à chaque élève son carnet de traces.
Distribuer à chaque élève :
– un bout de papier à masquer (collant)
– un carton de couleur 11 x 17 po
– une assiette d’encre de Chine (1 par table)
– un outil d’impression (réalisé jour 2)
– un petit contenant d’eau (1 pour 2 élèves)
– un morceau de papier brun
– un tablier.
.
14. Écrire son nombre sur un bout de papier à masquer (collant) et le placer sur le haut de son bureau, à droite.
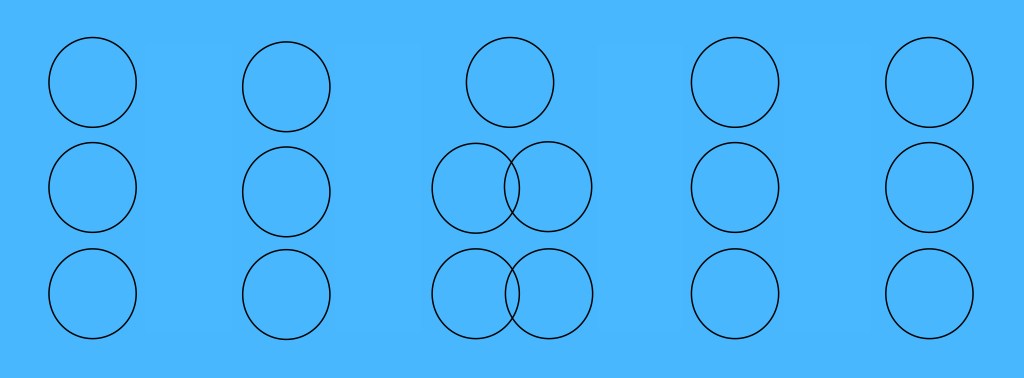
15. Sur un grand carton de couleur, tracer des cercles (voir, pages 6, 7 et 8) au crayon à mine.
.
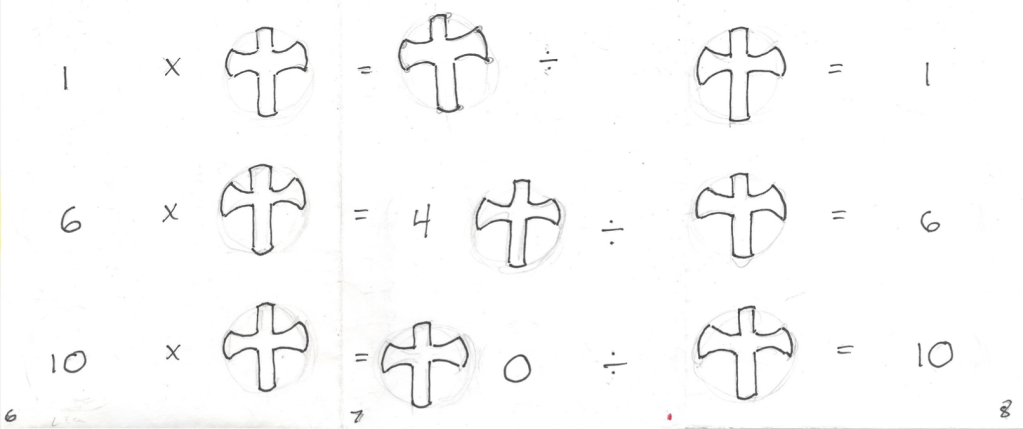
Espacer les cercles et y insérer les symboles suivants : x, =, ÷, =.
.
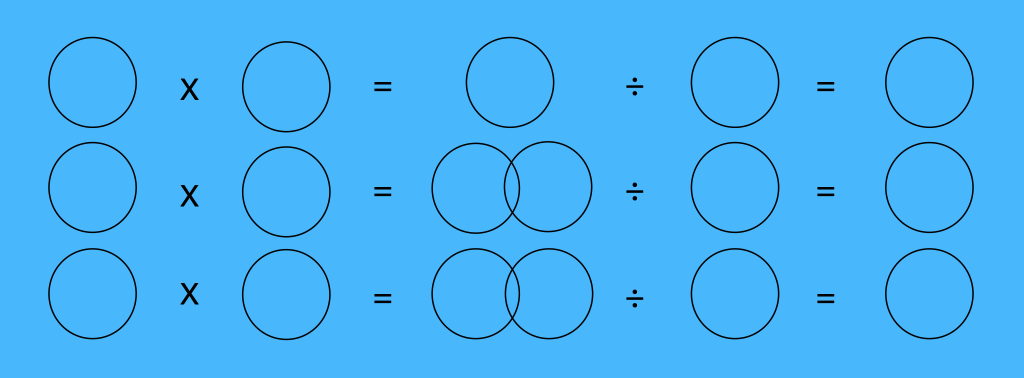
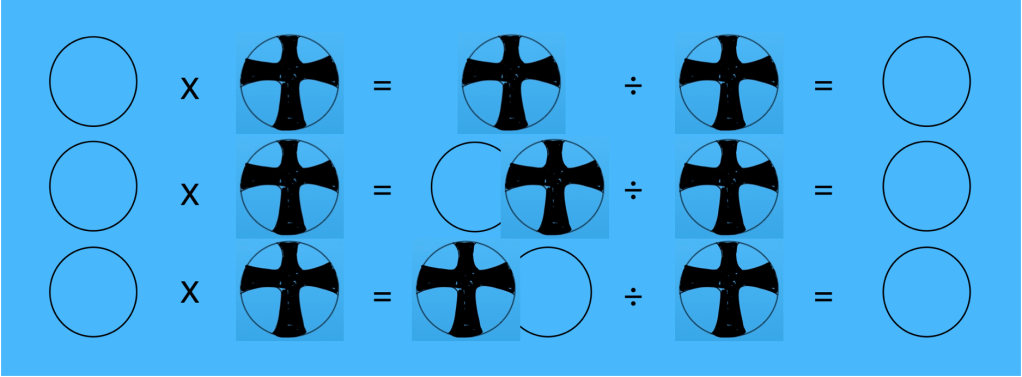
16. Démonstration — Tremper la partie supérieure (symbole) de l’outil d’imprimerie dans l’encre de Chine et imprimer son symbole sur du papier brun jusqu’à ce que le résultat soit satisfaisant. Imprimer son symbole au bon endroit sur son affiche.
.
17. Écrire les nombres manquants à l’intérieur des cercles au crayon à mine (l’encre de Chine ne pardonne pas). Tracer le 0 et le 1 au crayon-feutre noir.
.
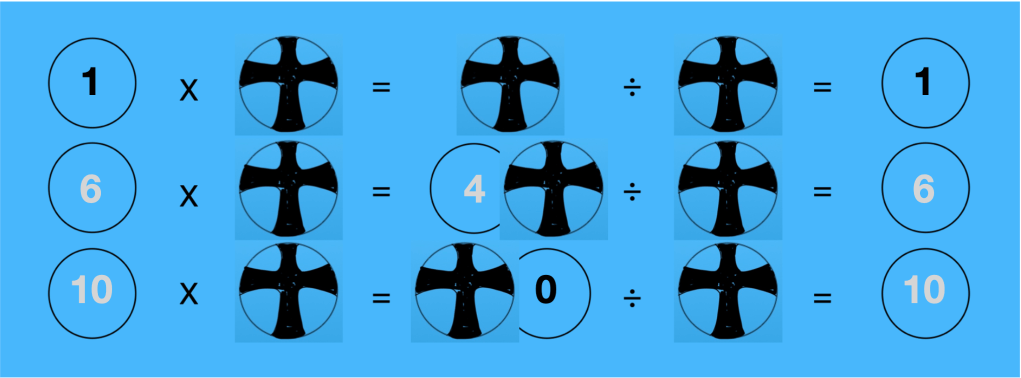
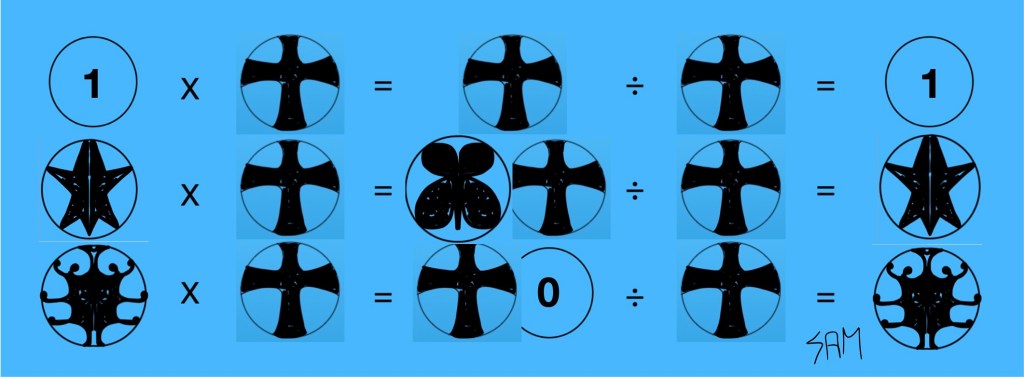
18. Trouver les détenteurs des nombres manquants et demander à l’auteur d’imprimer son symbole au bon endroit. Compléter les trois équations. Chaque élève aura besoin de ses pairs pour compléter son projet. Signer en bas à droite.
.
Réaliser une légende — Sur une autre affiche, imprimer les symboles utilisés en ordre croissant et écrire le nombre associé sous chaque symbole. Signer en bas à droite.
.
CONCLUSION
Réflexion et évaluation des mesures à prendre pour travailler en équipe ; décrire une situation de respect envers son groupe.
EXTENSIONS
1. Autoévaluation à partir d’une fiche.
2. Fixer les affiches au mur.
3. Réaliser une exposition : sur un carton blanc, imprimer son symbole à répétition de façon à recréer son nombre. Signer en bas à droite. Réaliser un travail de recherche et d’écriture sur la signification de son nombre : écrire une phrase ainsi que son nom sur une petite carte. Placer la petite carte sous la réalisation.
.
GLOSSAIRE
Asymétrie : absence de symétrie.
Encre de Chine : Réputée venir d’Orient, de Chine ou d’Inde, cette encre associe un pigment noir de carbone et un liant aqueux ; une encre noire utilisée pour l’écriture, le dessin et la peinture au lavis. Les Chinois utilisent également des bâtons d’encre de Chine de couleurs différentes (rouge, jaune, vert, bleu, etc.).
Forme tridimensionnelle ou 3D : sont des expressions qui caractérisent l’espace qui nous entoure, tel que perçu par notre vision, en termes de largeur, hauteur et profondeur.
Symbole : un concept, une représentation pensée chez un individu en particulier ou un groupe en général ; l’association faite par la pensée est déclenchée à partir des sens humains percevant quelque chose.
.
.
.
CONTENU D’APPRENTISSAGE – MINISTÈRE DE L’ÉDUCATION DU QUÉBEC
A la fin du 2e cycle, l’élève doit pouvoir :
Explorer l’arithmétique – sens des opérations sur des nombres naturels : choix de l’opération ; multiplication, division ; opérations sur des nombres naturels : approximation du résultat d’une opération : addition, soustraction, multiplication, division ; répertoire mémorisé : multiplications (1 x 1 à 12 x 12) en lien avec les divisions correspondantes.
COMPÉTENCE 2 – Raisonner à l’aide de concepts et de processus mathématiques
Cheminement de l’élève : il poursuit sa démarche d’appropriation de la terminologie, du symbolisme, des concepts et des processus mathématiques.
Composante de la compétence – Appliquer des processus mathématiques appropriés à la situation
Critères d’évaluation
- Analyse adéquate d’une situation d’application
- Application adéquate des processus retenus
Attentes de fin de cycle : sans pouvoir vraiment l’expliquer, il sait reconnaître les situations où l’utilisation de la technologie est indiquée.
COMPÉTENCE TRANSVERSALE 5 – Se donner des méthodes de travail efficaces
Évolution de la compétence : il fait preuve d’autonomie dans la définition de l’ensemble de sa démarche. Il sait trouver des façons originales d’atteindre ses buts.
Composante de la compétence – Analyser la tâche à accomplir : s’approprier l’objectif à atteindre ; comprendre les consignes et visualiser les éléments de la tâche ; situer le contexte de la tâche.
Critères d’évaluation
- Compréhension de la tâche à réaliser
- Exécution de la tâche
DOMAINE GÉNÉRAL DE FORMATION – Vivre ensemble et citoyenneté
Intention éducative
Permettre à l’élève de participer à la vie démocratique de l’école ou de la classe et de développer des attitudes d’ouverture sur le monde et de respect de la diversité.
Axe de développement – Engagement dans l’action dans un esprit de coopération et de solidarité : dynamique d’entraide avec les pairs.
LIEN CULTUREL – Enseignement traditionnel – Organisation partage – Production Manitu inc. Durée : 4 min 32 s.
LIENS ARTISTIQUES
La formation en arts plastiques alphabétise visuellement l’élève, développe son potentiel créateur au regard du monde visuel et ses habiletés à symboliser, à exprimer et à communiquer par le biais de l’image.
À la fin du 2e cycle, l’élève doit pouvoir :
Imprimer (objets divers avec encre).
Tracer à main levée (crayon-feutre).
COMPÉTENCE 1 – Réaliser des créations plastiques personnelles
Cheminement de l’élève : il transforme des matériaux dont l’utilisation est plus exigeante. Il diversifie son utilisation du langage plastique et exploite des agencements cohérents des éléments dans l’espace, tout en enrichissant ses idées de création grâce au partage avec les autres.
Composante de la compétence – Organiser les éléments résultant de ses choix
Critères d’évaluation
- Utilisation pertinente de gestes transformateurs spontanés et précis
- Relation entre sa réalisation et la proposition de création
Attentes de fin de cycle : sa réalisation résulte de gestes spontanés et précis, d’une utilisation pertinente du langage plastique et d’une organisation cohérente des éléments qui la composent.
OBJECTIFS PÉDAGOGIQUES INNUS
Par Anne-Marie André, Uashat (Québec)
OBJECTIF GLOBAL
Les objectifs pédagogiques innus consistent à susciter chez l’enfant la connaissance et le respect de son groupe ethnique, de son environnement et de ses traditions et favoriser la découverte des divers aspects de la vie innue d’hier et d’aujourd’hui.
OBJECTIF GÉNÉRAL
1. Connaître et respecter son groupe
OBJECTIF TERMINAL
1.8 Trouver des moyens de respecter son groupe
1.8.1 Décrire une situation de respect envers son groupe.
Tous droits réservés © 2016 ETAPMANITU
.
ETAPMANITU 