LE POLYÈDRE PAR LE SCHÉMA
PROJET
Réaliser une boite et créer des motifs à la manière des artistes issus des Premières Nations.
LE CUBE – Carton blanc, 8,5 x 11 pouces.
.
.
.
5e– 6e année, classe de Zina Kessir, école St-Pierre-Claver, Montréal (Québec), 2021-2022
.
MATÉRIEL
LE MATÉRIEL D’ART EST FOURNI PAR ETAPMANITU
1. Papier régulier, 11 x 17 po (1 par élève)
2. Crayon à mine, gomme à effacer et aiguisoir (1 par élève)
3.Crayon-feutre noir à pointe fine et régulière (1 par élève)
4. Carton blanc, 11 x 12 pouces (1 par élève)
5. Crayons-feutres de couleurs variées (3 par élève)
6. Règle et rapporteur d’angles (1 par élève)
7. Bâton de colle (1 par élève)
.
LANGAGE PLASTIQUE
Couleurs primaires : jaune primaire, cyan, magenta
Couleurs secondaires : orangé, vert, violet
Forme : angulaire
Lignes : courte, longue, large, étroite
Matériau : carton
Organisation de l’espace : répétition, alternance
Technique : dessin
Volume : forme tridimensionnelle
Vocabulaire : cube, polyèdre convexe, degré (angle), rapporteur d’angles, relation d’Euler
.
OUTILS PÉDAGOGIQUES
Vidéo sur le mode de vie innu – Enseignement traditionnel – Production Manitu inc.
Message – Durée : 2 min 33 s.
.
Motifs utilisés par les artistes issus des Premières Nations
.
.
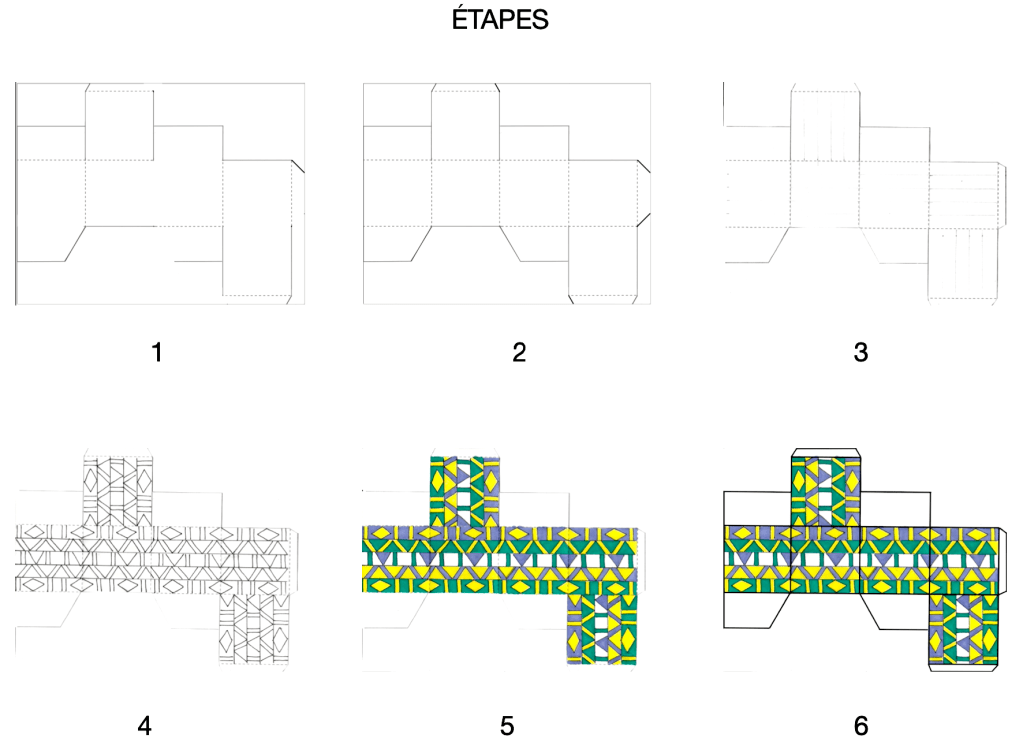
Documents (à imprimer, à couper et à coller)
.
.
.
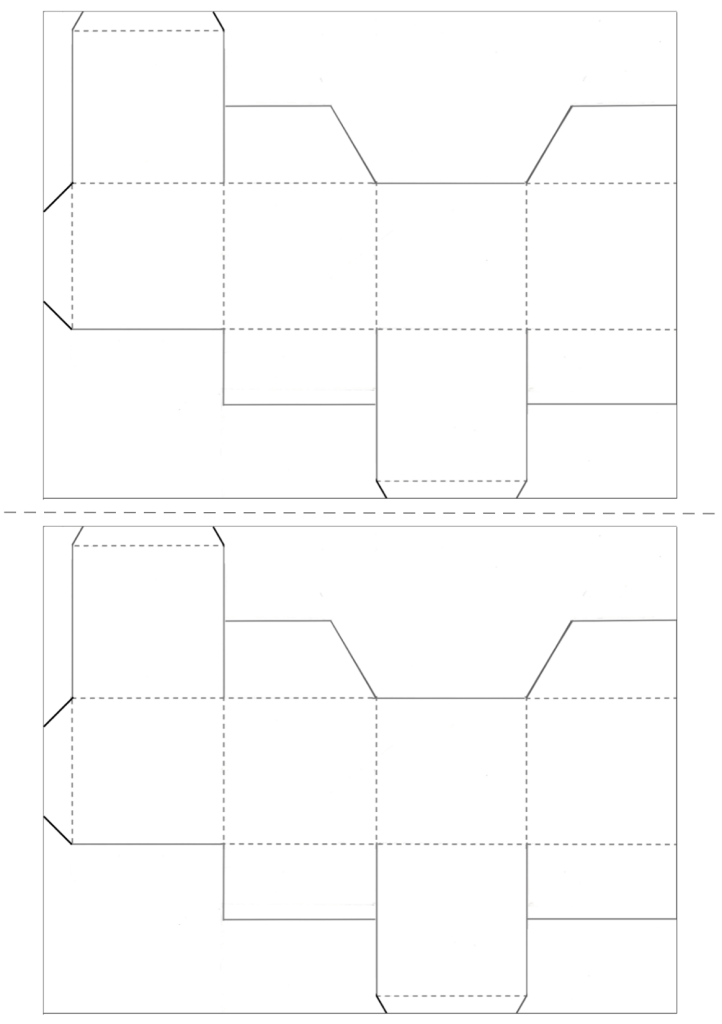
Schéma inachevé
.
.
.
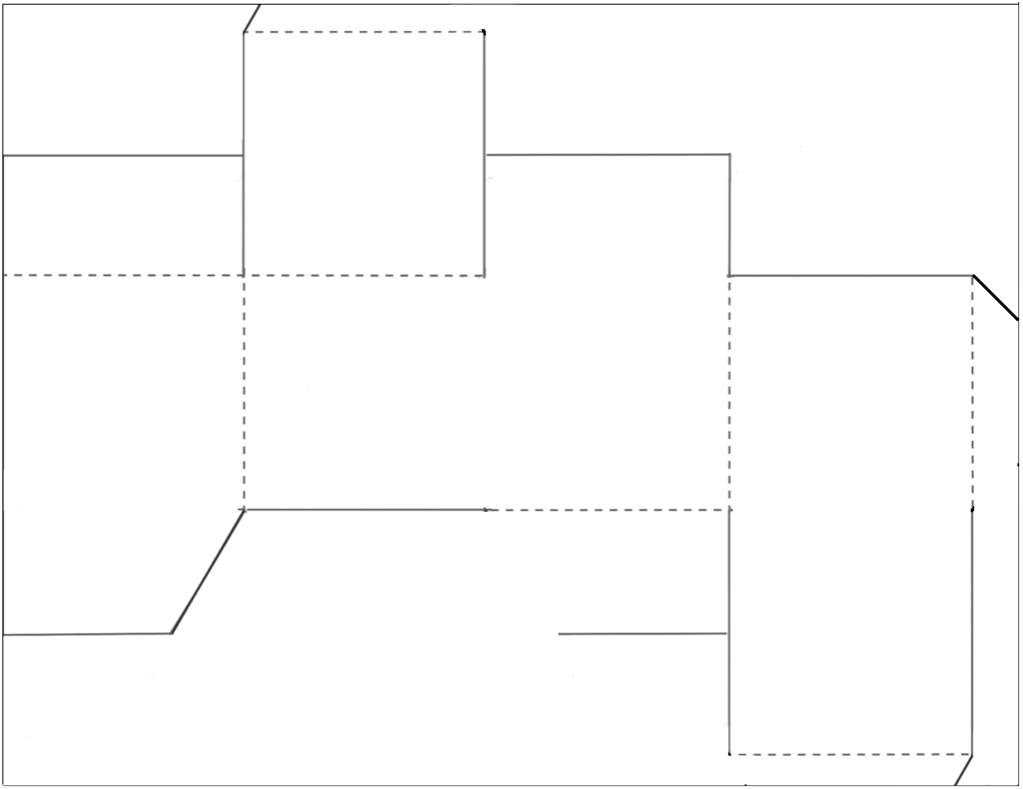
Carnet de traces
.
.
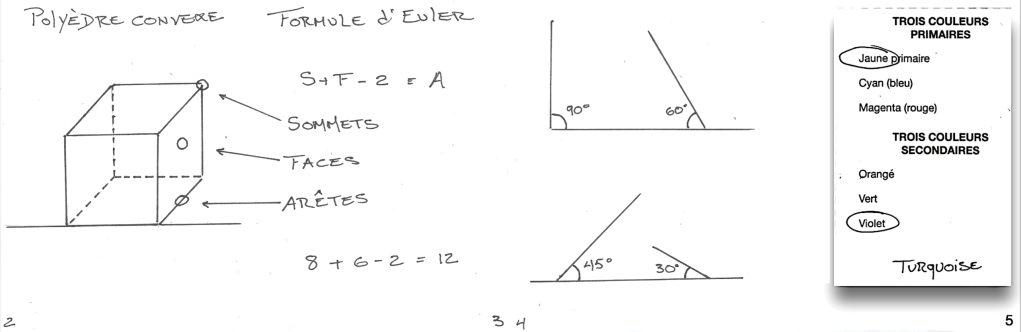
Ce projet est financé par le ministère de l’Éducation et de l’Enseignement supérieur du Québec.
.
.
CONTENU DU CARNET DE TRACES
Les élèves fabriquent un carnet de traces de 8 pages et compilent les informations suivantes :
PAGE COUVERTURE : écrire son nom en bas, au centre ; dessiner un cube au centre de la page ; tracer cinq lignes à l’horizontale sur une face ; réaliser quatre motifs ; écrire « cube » en haut de la page.
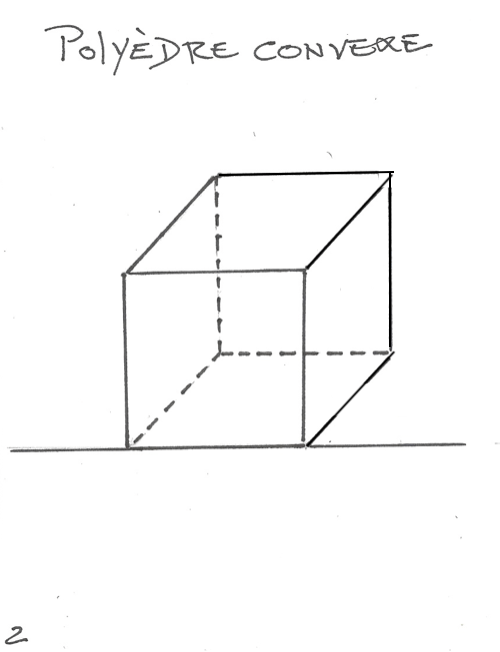
Page 2 : écrire « Polyèdre convexe » en haut de la page ; dessiner un cube ; indiquer les angles.
Page 3 : écrire la formule d’Euler ainsi que la réponse ; tracer des flèches pour indiquer l’emplacement d’un sommet, d’une face et d’une arête sur le cube de la page 2.
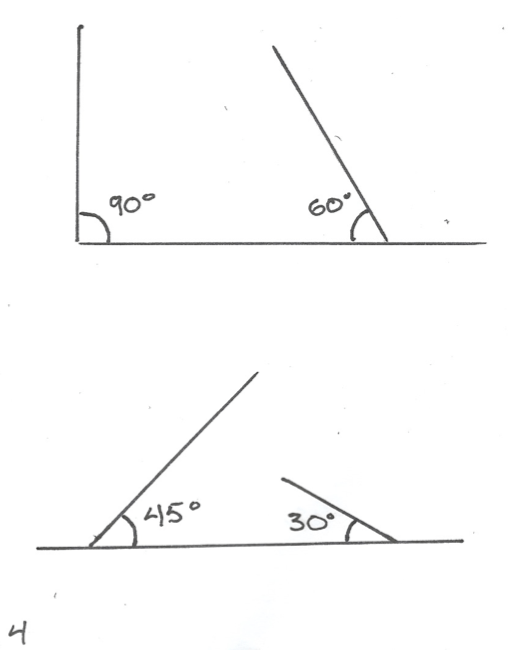
Page 4 : tracer deux lignes horizontales ; rapporter un angle à 90° et un autre à 60° sur la première ligne ; rapporter un angle à 45° et un autre à 30° sur la deuxième ligne.
Page 5 : coller une photocopie de la liste des couleurs primaires et secondaires ; entourer le nom de deux couleurs, soit une primaire et une secondaire.
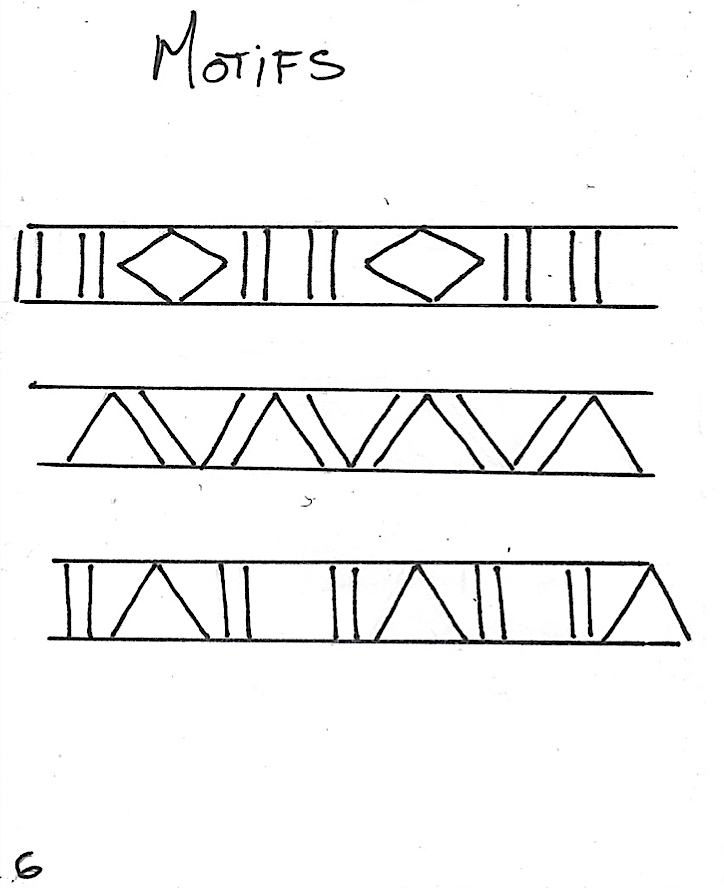
Page 6 : tracer six lignes horizontales ; dessiner trois motifs à l’intérieur des lignes.
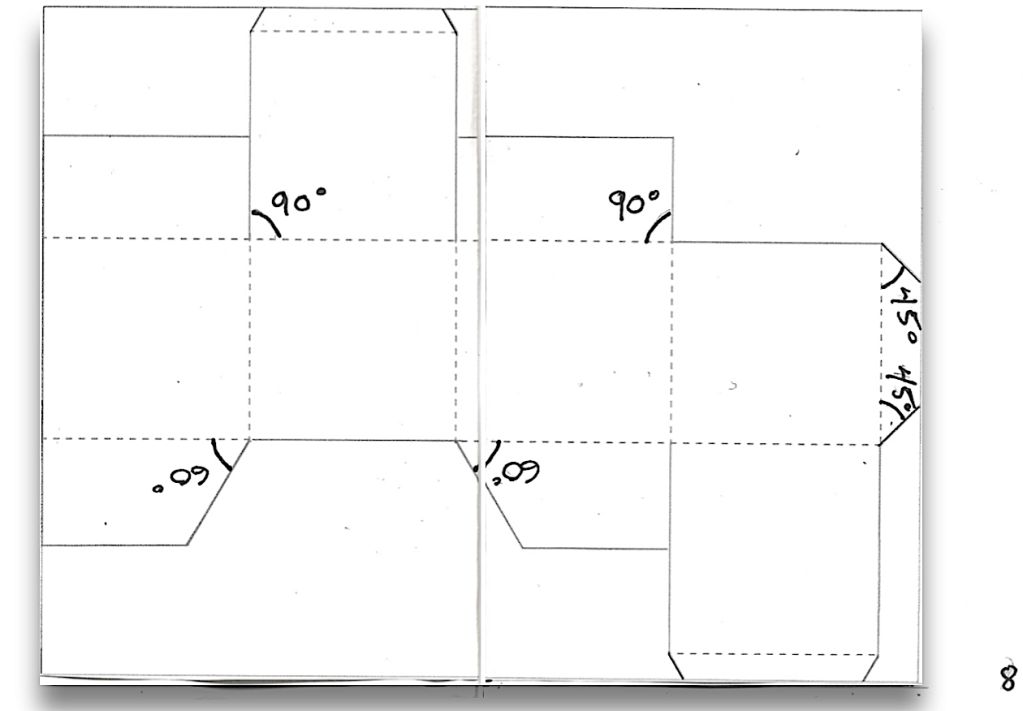
Page 7 : coller une photocopie du schéma d’une boite ; écrire les angles.
Page 8 : suite de la page 7.
Démonstration — Réalisation d’un carnet de traces – Durée : 48 s.
.
ÉTAPES DU COURS
Jour 1
PRÉPARATION
Préparer sur le TBI (tableau blanc interactif)
– la vidéo sur le mode de vie innu pour le visionnement
– la réalisation du projet en six étapes pour consultation.
.
Distribuer à chaque élève un papier régulier de 11 x 17 pouces.
.
1. Présentation de l’artiste et du projet. Qu’est-ce qu’un polyèdre ? C’est un solide de l’espace de dimension 3 dont la frontière est la réunion de parties de plans. (Ces parties sont les faces, leurs côtés communs sont les arêtes, dont les points communs sont les sommets du polyèdre.) Consulter la réalisation du projet en six étapes (sur le TBI).
2. Visionner la vidéo sur le mode de vie innu — Message — Production Manitu inc. Durée : 2 min 33 s. Comment les nomades communiquaient-ils entre eux ? Par la disposition de quelques branches.
3. L’élève réalise un carnet de traces en manipulant et en pliant un papier de 11 x 17 pouces, en 8 carrés égaux. Il repère la page couverture et écrit son nom au bas de la page. Il numérote ensuite les pages de 2 à 8 dans les coins extérieurs.
4. Dessiner un cube au tableau — Tracer une ligne horizontale et faire un point à gauche sur la ligne. Rapporter un angle à 90°, calculer 1,5 pouce vers le haut et faire un point. Calculer 1,5 pouce vers la droite et rapporter un autre angle à 90°. Calculer 3/4 de pouce et tracer une ligne (très pâle) parallèle à la ligne horizontale. Tracer ensuite un angle à 45° (du point gauche vers le haut). Rapporter les lignes et réaliser un cube. Tracer des pointillés sur les lignes de façon à créer l’illusion d’un solide. Dessiner à la page 2. Écrire « Polyèdre convexe » en haut de la page.
.
5. Qu’est-ce que la formule d’Euler ? C’est une relation mathématique qui permet de mettre en relation le nombre d’arêtes, de faces et de sommets d’un polyèdre. Pour la reconnaitre, elle est nommée selon le mathématicien suisse qui en est le créateur : Leonhard Euler. Écrire « Formule d’Euler » en haut de la page 3 et la formule : S + F – 2 = A (Sommets + Faces – 2 = Arêtes). Trouver et écrire la réponse au bas de la page : 8 + 6 – 2 = 12.
.
Entre le jour 1 et le jour 2
– L’enseignant s’assure de la compréhension de l’élève et vérifie que la collecte de l’information est conforme aux attentes : cube, éléments clairement indiqués par des flèches (page 2), formule de la relation d’Euler et réponse (page 3).
Jour 2
PRÉPARATION
Préparer sur le TBI le tableau de motifs à la manière des artistes issus des Premières Nations.
.
Imprimer et couper le schéma d’une boite, format env. 5 x 7 po (1 par élève).
.
Redonner à chaque élève son carnet de traces.
Distribuer à chaque élève :
– une photocopie du schéma d’une boite
– un crayon-feutre noir (pointe fine)
– un bâton de colle.
.
6. Démonstration — Tracer une ligne horizontale au centre de la page 4. Estimation : pointer à env. 1 pouce à partir de la gauche, reproduire à partir de la droite. Rapporter un angle à 90° (à gauche) et un autre à 60° (à droite). Tracer une autre ligne horizontale au bas de la page et rapporter un angle à 45° (à gauche) et un autre à 30° (à droite).
.
7. Qu’est-ce qu’un schéma ? C’est une figure donnant une représentation simplifiée et fonctionnelle (d’un objet, d’un processus…). Coller une photocopie du schéma d’une boîte, pages 7 et 8. Trouver et écrire deux angles à 90°, deux angles à 60° et deux autres à 45°. Dessiner au tableau — Tracer les lignes formant le schéma d’une boite et indiquer les angles.
.
8. Pointer à 1 pouce à partir d’en bas et tracer une ligne horizontale au crayon à mine, page 6. Pointer à chaque pouce vers le haut et tracer six lignes horizontales. À l’aide d’un document sur les motifs (sur le TBI), choisir et tracer quatre motifs à l’intérieur des lignes horizontales.
.
9. Démonstration — Ouvrir complètement le carnet de traces ; glisser une équerre ou une règle pour rapporter les lignes et les angles de la page 2 sur la page couverture.
.
Dessiner un cube de 1,5 pouce sur la page couverture.
.
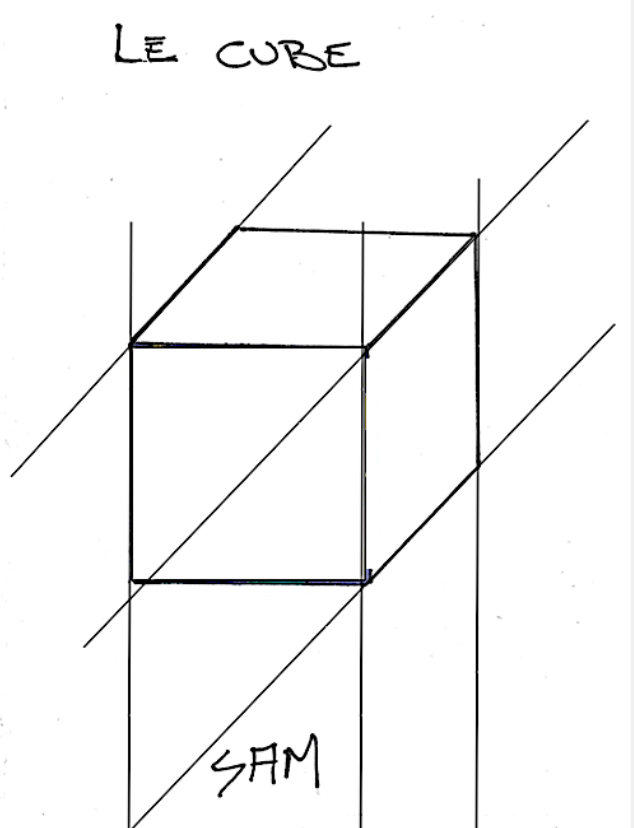
10. Pointer à tous les 0,5 pouces et tracer cinq lignes à 90° sur une face. Dessiner les motifs de la page 6. Retracer les motifs et les lignes de contour du cube au crayon-feutre noir à pointe fine. (Pour éviter de laisser des tâches, placer un papier entre la page couverture et la page 2.) Effacer les traces de crayon à mine. NE PAS COLORIER L’INTÉRIEUR DES MOTIFS.
.
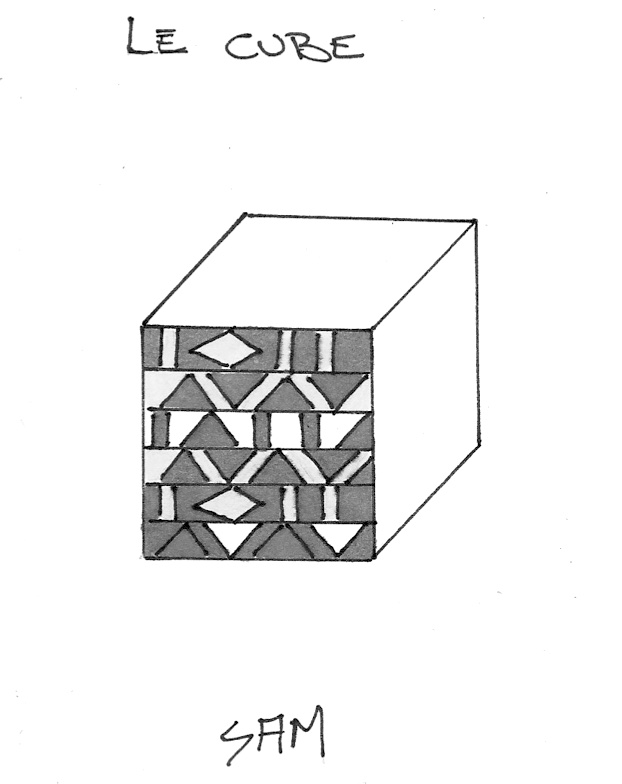
Entre le jour 2 et le jour 3
– L’enseignant s’assure que les éléments suivants figurent dans les carnets de traces : angles à 90°, 60°, 45° et 30° (page 4), huit lignes horizontales et quatre motifs autochtones (page 6), deux angles à 90°, deux à 60° et deux à 45° (pages 7 et 8), cube et motifs sur une face (page couverture).
– L’élève termine la page couverture du carnet de traces.
Jour 3
PRÉPARATION
Préparer sur le TBI
– le tableau des couleurs primaires et secondaires pour consultation
.
– la réalisation du projet en six étapes pour consultation.
.
Imprimer et couper la liste des trois couleurs primaires et secondaires, format env. 4 x 3 po (1 par élève).
.
Imprimer le schéma inachevé de 8,5 x 11 po (1 par élève).
.
Rassembler des crayons-feutres en trois associations de couleurs, soit : jaune et violet + turquoise ; magenta et vert + ocre ; cyan et orangé + vert pomme (3 par élève).
Redonner à chaque élève son carnet de traces.
Distribuer à chaque élève :
– une photocopie de la liste des trois couleurs primaires et secondaires
– deux crayons-feutres noirs (pointe fine et régulière)
– trois crayons-feutres (combinaison de trois couleurs)
– des ciseaux
– un bâton de colle.
.
11. Consulter le tableau des trois couleurs primaires et secondaires (sur le TBI). Quelles sont les trois couleurs primaires ? Jaune, cyan (bleu) et magenta (rouge). Et les trois couleurs secondaires ?Vert, orangé, violet. Coller une photocopie à la page 2. Choisir et entourer une couleur primaire. Comment trouver les couleurs qui ont le plus d’impact lorsqu’elles sont placées côte à côte ? Par exemple : prenons le magenta (rouge). Quelles sont les deux autres couleurs ? Le jaune et le cyan (bleu). Quand on les mélange, on obtient du vert. Le vert est donc la couleur complémentaire du magenta. Entourer une des trois couleurs secondaires. (Ces deux couleurs seront mises en valeur dans la réalisation finale.)
.
12. Qu’est-ce qu’une couleur tertiaire ? C’est une association des couleurs primaires et secondaires à parts égales. Combien y en a-t-il ? Six. Écrire trois associations de couleurs au tableau, soit : jaune et violet = turquoise ; magenta et vert = ocre ; cyan et orangé : vert pomme. (Ces trois couleurs seront mises en valeur dans la réalisation finale.) Écrire la troisième couleur en bas de la page 5. Faire un essai sur la page couverture : ajouter les trois couleurs (association) en alternance (laisser des espaces blancs pour créer de la lumière). Cet exercice permettra d’améliorer le résultat final.
.
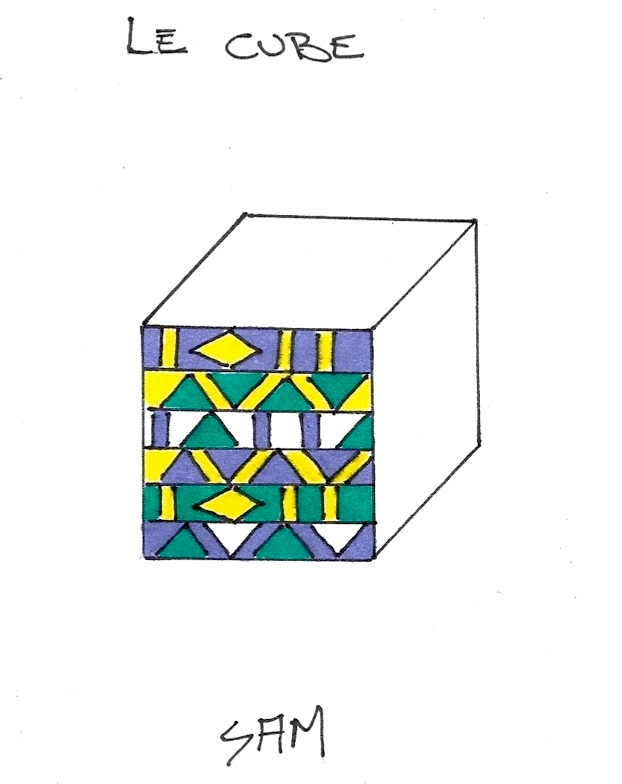
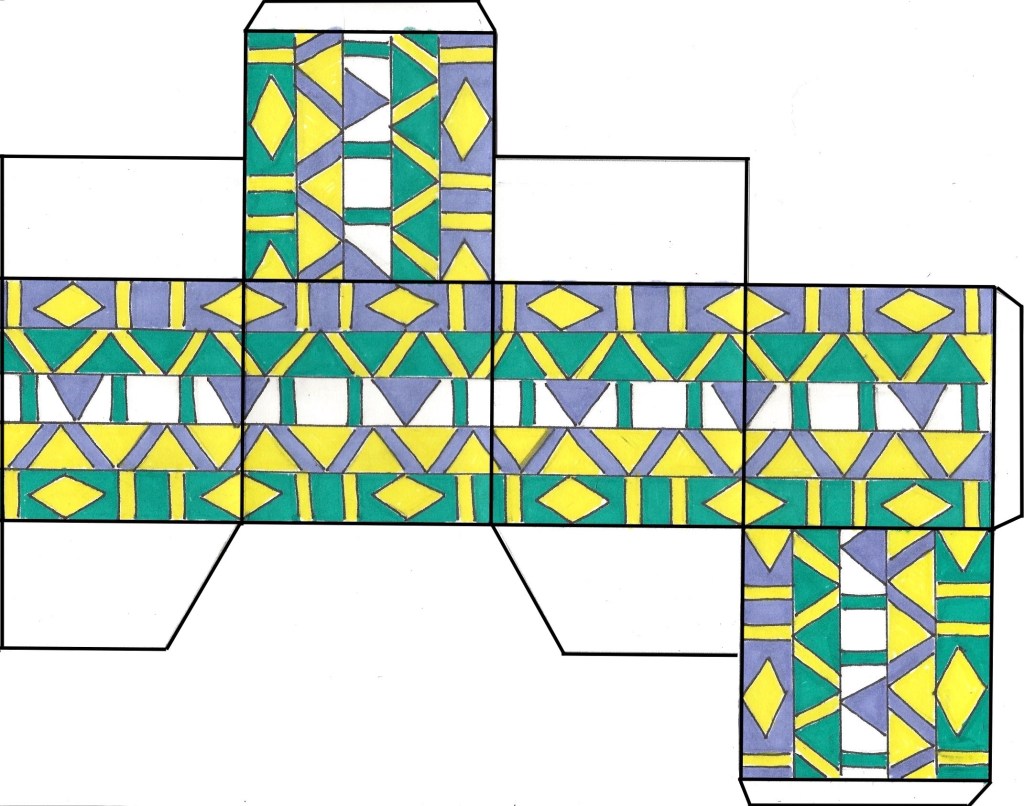
13. Terminer le schéma d’une boite — À l’aide du schéma des pages 7 et 8, tracer les lignes manquantes au crayon à mine sur un schéma inachevé : lignes pointillées et autres. Découper sur les lignes. Ne pas découper sur les lignes pointillées.
14. Pointer à tous les 0,5 pouce et tracer quatre lignes à 90° à l’horizontale sur les quatre faces du centre du schéma (cube) et une autre série de quatre à l’horizontale ou à la verticale OU ENCORE à la diagonale à 45° sur les faces de côtés (dessous et dessus du cube).
.
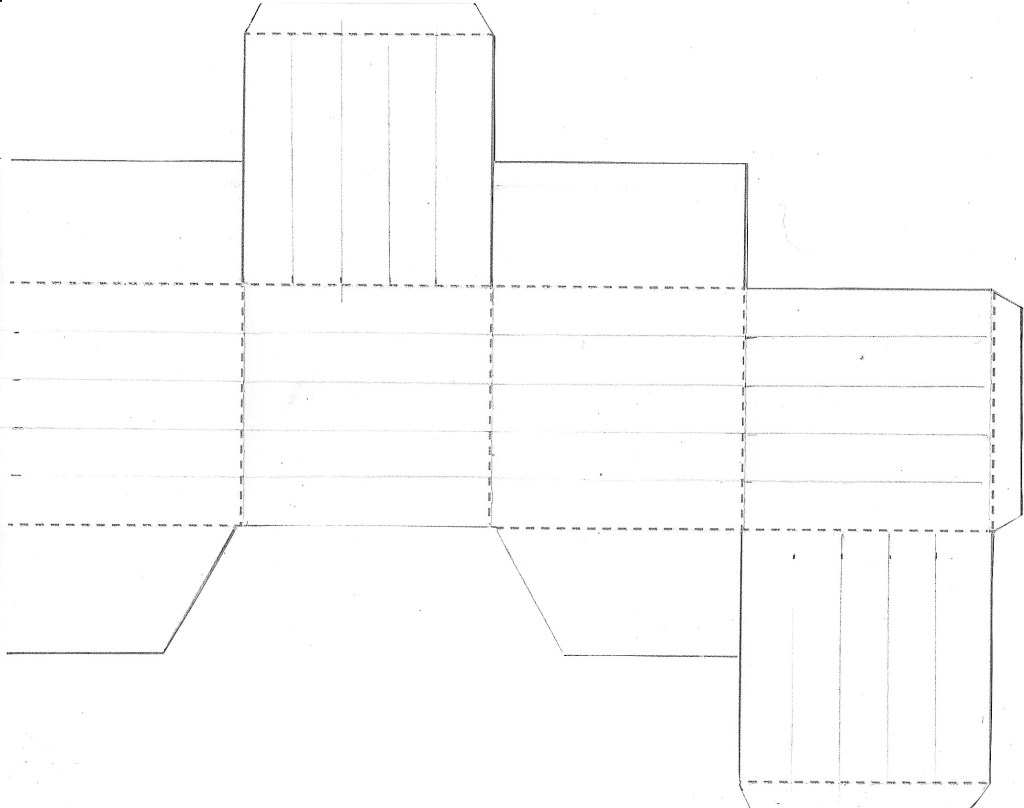
15. Dessiner les motifs choisis à l’intérieur des lignes (voir page couverture), au crayon-feutre noir (pointe fine). *Bien qu’il y ait six motifs sur la page couverture, il n’y en a que cinq sur la boite (omettre une ligne qui ne fonctionne pas très bien avec les autres permet d’améliorer l’effet visuel).
.
16. Ajouter trois couleurs (associations) telles que sur la page couverture.
.
17. Tracer les lignes de contour au crayon-feutre noir. (On peut choisir de tracer les lignes de contour de tous les motifs au crayon-feutre noir.)
.
18. Ouvrir des ciseaux de façon à utiliser une des deux lames, tenir tel un crayon et appuyer sur les lignes pointillées. NE PAS APPUYER TROP FORT. Plier la boite sur les pointillés et vers l’intérieur de façon à obtenir un cube. Coller la petite bande à droite du schéma vers l’intérieur de façon à ce que le cube reste en place. Appliquer du papier collant, si nécessaire.
.
CONCLUSION
Réflexion et évaluation des mesures à prendre pour consolider sa compréhension des concepts et des processus mathématiques.
EXTENSIONS
1. Autoévaluation à partir d’une fiche.
.
2. Suspendre les cubes : couper des bouts de ficelles de différentes longueurs ; ouvrir le couvercle des boites, coller un bout de ficelle à l’intérieur puis refermer de façon à emprisonner la ficelle ; fixer au plafond ou au mur.
5e– 6e année, classe de Zina Kessir, école St-Pierre-Claver, Montréal (Québec), 2021-2022
.
3. Réaliser des prismes à bases triangulaires et rectangulaires.
4. Réaliser une frise : dessiner des motifs sur des bandes de carton blanc ; ajouter trois couleurs en utilisant la technique apprise ; fixer autour du cadre d’une porte ou d’une fenêtre ou encore, sur les murs près du plafond.
GLOSSAIRE
Culture : accumulation personnelle d’éléments qui guident (ou déterminent) le comportement d’un humain dans un environnement donné.
Forme : agencement des structures.
Équerre : instrument destiné à tracer des angles droits ou à élever des perpendiculaires.
Perpendiculaire : qui forme un angle droit.
Polyèdre : solide de l’espace de dimension 3 dont la frontière est réunion de parties de plans. (Ces parties sont les faces, leurs côtés communs sont les arêtes, dont les points communs sont les sommets du polyèdre.)
Relation d’Euler : relation mathématique qui permet de mettre en relation le nombre d’arêtes, de faces et de sommets d’un polyèdre. Pour la reconnaitre, elle est nommée selon le mathématicien qui en est le créateur : Leonhard Euler.
Schéma : figure donnant une représentation simplifiée et fonctionnelle (d’un objet, d’un processus…).
.
.
CONTENU D’APPRENTISSAGE – MINISTÈRE DE L’ÉDUCATION DU QUÉBEC
Géométrie et sens spatial
– Solides : reconnaissance du développement de polyèdres convexes ; expérimentation de la relation d’Euler (relation entre les faces, les sommets et les arêtes d’un polyèdre convexe)
– Figures planes : mesure d’angles en degrés à l’aide d’un rapporteur d’angles
– Angles estimation et mesurage : degré
À la fin du 3e cycle, l’élève doit pouvoir :
Cueillir et traiter l’information : collecter les données.
Organiser l’information : arranger les données en construisant des tableaux, des listes, des graphiques ou en produisant un texte.
COMPÉTENCE 2 – Raisonner à l’aide de concept et de processus mathématiques
Cheminement de l’élève : il approfondit sa compréhension du sens des nombres et des opérations. Il poursuit l’étude d’objets géométriques selon leurs attributs, la construction de relations géométriques, l’expérimentation d’activités liées au hasard et l’interprétation de données statistiques. Il évalue la pertinence de l’utilisation de la technologie lors d’une activité. Il consolide sa compréhension des concepts et des processus mathématiques.
Composante de la compétence – Appliquer des processus mathématiques appropriés à la situation
Critères d’évaluation
- Analyse adéquate d’une situation d’application
- Application adéquate des processus retenus
Attentes de fin de cycle : à l’aide de matériel concret et de schémas, il commence à additionner et à soustraire des fractions, et à multiplier des fractions par des nombres naturels. Il peut décrire et classifier des figures planes, reconnaître le développement de polyèdres convexes, estimer, mesurer ou calculer des longueurs, des surfaces, des volumes, des angles […]. Il peut produire des frises et des dallages par réflexion et translation, comparer les résultats possibles d’une expérience aléatoire aux résultats théoriques connus […].
COMPÉTENCE TRANSVERSALE 5 – Se donner des méthodes de travail efficaces
Évolution de la compétence : il parvient à s’approprier différentes démarches et méthodes et à les transposer de manière appropriée dans diverses situations. Il accepte d’investir temps et énergie en vue de l’objectif à atteindre.
Composante de la compétence – Accomplir la tâche : gérer son matériel et son temps, réajuster ses actions au besoin ; mener sa tâche à terme ; découvrir le plaisir et la satisfaction du travail achevé et bien fait.
Critères d’évaluation
- Compréhension de la tâche à réaliser
- Persévérance et ténacité dans l’action
DOMAINE GÉNÉRAL DE FORMATION – Orientation et entreprenariat
Intention éducative
Offrir à l’élève des situations éducatives lui permettant d’entreprendre et de mener à terme des projets orientés vers la réalisation de soi et l’insertion dans la société
Axe de développement – Conscience de soi, de son potentiel et de ses modes d’actualisation : connaissance de ses talents, de ses qualités, de ses intérêts et de ses aspirations personnelles et professionnelles ; sens du travail scolaire, goût du défi et sentiment de responsabilité face à ses succès et à ses échecs.
LIEN CULTUREL – Ouverture sur la vidéo – Enseignement traditionnel – Message – Production Manitu inc. Durée : 2 min 33 s.
LIENS ARTISTIQUES
La formation en arts plastiques alphabétise visuellement l’élève, développe son potentiel créateur au regard du monde visuel et ses habiletés à symboliser, à exprimer et à communiquer par le biais de l’image.
À la fin du 3e cycle, l’élève doit pouvoir :
Découper, enduire une surface de colle (carton).
Plier (carton).
Tracer à main levée (crayon-feutre).
COMPÉTENCE 1 – Réaliser des créations plastiques personnelles
Cheminement de l’élève : c’est de façon plus consciente que l’élève utilise chacune des étapes de la démarche de création. À la suite d’expérimentations variées, il transforme des matériaux de façon plus contrôlée. Il diversifie son utilisation du langage plastique et exploite des agencements complexes et variés des éléments dans l’espace. Ce faisant, il adapte de manière personnelle les idées de création qu’il a retenues au cours du développement de la proposition.
Composante de la compétence – Exploiter des idées de création inspirées par une proposition
Critères d’évaluation
- Utilisation pertinente de gestes transformateurs spontanés, précis et contrôlés
- Organisation complexe des éléments
Attentes de fin de cycle : il utilise de façon consciente chacune des étapes de la démarche de création. Sa réalisation est guidée par des intérêts d’ordre social, affectif et cognitif. Elle est personnelle et traduit sa perception du réel. Elle résulte de gestes contrôlés […] et d’une organisation complexe des éléments qui la composent.
OBJECTIFS PÉDAGOGIQUES INNUS
Par Anne-Marie André, Uashat (Québec)
OBJECTIF GLOBAL
Les objectifs pédagogiques innus consistent à susciter chez l’enfant la connaissance et le respect de son groupe ethnique, de son environnement et de ses traditions et à favoriser la découverte des divers aspects de la vie innue d’hier et d’aujourd’hui.
OBJECTIF GÉNÉRAL
3. Apprendre les diverses traditions transmises par les Anciens
OBJECTI TERMINAL
3.1 Trouver les valeurs transmises par les Anciens
3.1.1 À l’aide d’exemples simples tirés de la vie quotidienne, trouver les valeurs véhiculées par les Anciens.
Tous droits réservés © 2016 ETAPMANITU
.
ETAPMANITU 